Inversis Schatz nach Paul Schatz

Der Künstler und Mathematiker Paul Schatz erkannte, dass man aus einem Würfel drei Elemente mit gleichem Volumen herausschneiden kann. Beim mittleren Teilstück handelt es sich um einen so genannten Kaleidozyklus, einen Ring aus sechs Dreieckspyramiden (s. Video). Diese Dreieckspyramiden sind durch Scharniergelenke miteinander verbunden und lassen sich ineinander verdrehen.

Aus einem Würfelgürtel wird Inversis Schatz

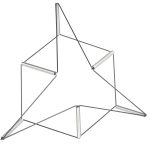
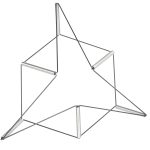
Schatz nannte die beiden äußeren geometrischen Objekte Riegelkörper und das innere Element Würfelgürtel. Letzteres wandelte er ab und verkaufte das daraus entstandene Produkt aus Draht unter dem Namen Inversis Schatz. Als Drahtgeflecht wird ein solcher Würfelgürtel auf sein Minimum reduziert. Umstülpbare Würfel kann man auch selbst basteln. Alle Informationen dazu finden Sie weiter unten.

Umstülpbare Würfel als Formwandler

Diesen Würfelgürtel kann man in einer unendlichen Folge umstülpen, verdrehen, umkrempeln und dabei zusehen, wie unterschiedliche Formen entstehen: Im Wechsel Würfel und Dreiecke, jedoch zum Teil unvollständig und angedeutet, als Hohlkörper, so dass die räumliche Vorstellungskraft des Betrachters gefordert ist und sich schulen lässt. Dies gilt vor allem für die die Version aus Draht, die Paul Schatz „Inversis Schatz“ nannte.

Aus dem umstülpbaren Würfel entsteht ein Oloid

Die Fläche, die in der Umstülpbewegung überstrichen wird, entspricht wiederum der eines Oloid, einem Wälzkörper, zu dem Sie im Video unten und hier einen ausführlichen Artikel mit weiteren Informationen finden. Beide Objekte sind wunderbare geometrische Spielereien.

Auch technische Anwendungen sind aus diesen geometrischen Spielereien entstanden und ihr Entdecker, Paul Schatz, hält Patente zu allerlei Erfindungen, die insbesondere mit dem Oloid in einem Zusammenhang stehen – Rührgeräte zum Beispiel. Paul Schatz studierte Mathematik, Maschinenbau und Astronomie – alles jedoch ohne Abschluss – bevor er sich der Kunst zuwandte und sich mit technischen Anwendungen zu seinen Entdeckungen befasste.

Der umstülpbare Würfel als Kaleidozyklus

Ganz vereinfacht betrachtet handelt es sich bei diesem Drahtgeflecht um eine Kette aus sechs speziellen Gliedern, die durch Scharniergelenke verbunden sind. Solche Ketten sind bekannt unter dem Begriff Kaleidozyklen, wenn die Glieder wie in diesem Fall aus Tetraedern konstruiert sind.

Tetraeder ist ein anderes Wort für Dreieckspyramide und darunter wiederum versteht man ein geometrisches Objekt, bei dessen Grundfläche es sich um ein Dreieck handelt und bei den drei Seitenflächen ebenfalls. Dieses Objekt ist die einfachste Variante eines Kaleidozyklus – einfacher geht es nicht, nur komplizierter und mit mehr Gliedern. Mehr zum Thema Kaleidozyklen erfahren Sie hier.

Inversis Schatz – nahe an der Perfektion

Das Besondere außerdem: Die Dreieckspyramiden sind nur angedeutet, tatsächlich handelt es sich nur um verdrehte Rechtecke. Bei jeder einzelnen Dreieckspyramide fehlen also zwei der sechs Kanten. Einen vollständigen Würfelgürtel aus sechs Gliedern kann man zum Beispiel im Gießener Mathematikum bewundern. Der Inversis Schatz ist die einfachste Variante eines Kaleidozyklus – einfacher geht es nicht, nur komplizierter und mit mehr Gliedern.

Antoine de Saint-Exupéry hat einst festgestellt, dass „Perfektion nicht dann erreicht ist, wenn man nichts mehr hinzufügen, sondern nichts mehr weglassen kann“. So gesehen kommt dieses schlichte Drahtgeflecht der Perfektion sicherlich sehr nahe.

Den umstülpbaren Würfel selbst basteln

Selbst bauen kann man verschiedene Objekte nach Paul Schatz ebenfalls. Bastelbögen zum Download als PDF finden Sie hier:

Der umstülpbare Würfel
Riegelkörper Variante I
Riegelkörper Variante II

Außerdem befinden sich auf der Seite von Frank Zahaurek noch viele andere spannende Informationen zum umstülpbaren Würfel sowie dem Oloid.