Der Begriff Kleinsche Flasche steht für ein geometrisches Objekt, das Mathematiker liebevoll als nicht-orientierbare zweidimensionale differenzierbare Mannigfaltigkeit
Der Begriff Kleinsche Flasche steht für ein geometrisches Objekt, das Mathematiker liebevoll als nicht-orientierbare zweidimensionale differenzierbare Mannigfaltigkeit bezeichnen. Zu Deutsch bedeutet dies, dass im Fall einer Kleinschen Flasche das Innere zugleich das Äußere ist oder anders gesagt: Man kann vom vermeintlich Inneren auf die Außenseite wechseln, ohne dabei über eine Kante zu gehen wie etwa bei einem Trinkbecher.
bezeichnen. Zu Deutsch bedeutet dies, dass im Fall einer Kleinschen Flasche das Innere zugleich das Äußere ist oder anders gesagt: Man kann vom vermeintlich Inneren auf die Außenseite wechseln, ohne dabei über eine Kante zu gehen wie etwa bei einem Trinkbecher.
Deshalb ist es nicht möglich, Inneres und Äußeres zu unterscheiden. Dieses Phänomen ist nicht nur für Topologen interessant, sondern an sich sehr faszinierend. Mathematisch betrachtete hat die Kleinsche Flasche damit auch kein Volumen.
Die hier gezeigte Kleinsche Flasche gibt es im Shop zu kaufen.
Felix Klein und die Kleinsche Flasche
Benannt ist die Kleinsche Flasche nach dem deutschen Mathematiker Felix Klein, der diese topologische Form 1882 als Erster untersuchte.
Eine vergleichbare und ebenfalls sehr interessante Figur ist das Möbiusband, das man erhält, wenn man einen Papierstreifen einmal verdreht und dann zusammenklebt. Auch hier ist es dann möglich, von innen nach außen zu wechseln, ohne dabei über eine Kante zu gehen.
Das Möbiusband ist nach dem Astronomen und Mathematiker August Ferdinand Möbius (1790 – 1868) benannt, der es im Jahr 1858 beschrieb.
Die Verbindung von Möbiusband und Kleinscher Flasche
Im Video unten kann man sehen, wie aus einer Kleinschen Flasche ein Möbiusband entsteht. Man kann eine Kleinsche Flasche jedoch auch aus einem einfachen, zweidimensionalen Quadrat erzeugen. Man klappt dieses zusammen, so dass man eine Röhre erhält, öffnet die Enden ein wenig und lässt die Röhre sich selbst durchdringen. Wie das genau aussieht, wird ebenfalls sehr schön in dem Video unten gezeigt. Sägt man eine Kleinsche Flasche auseinander, erhält man zwei Möbiusbänder.
Was ist Topologie?
Phänomene wie das Möbiusband und die Kleinsche Flasche gehören in die Topologie. Diese beschäftigt sich mit Formen, die sich nicht ändern, selbst wenn sie beispielsweise gedehnt oder verdreht werden. Zerstört werden dürfen sie bei diesem Prozess jedoch nicht und die Formänderung muss stetig vor sich gehen.
Die Kleinsche Flasche in vier Raumdimensionen
Mathematiker weisen gerne darauf hin, dass eine Selbstdurchdringung einer Kleinschen Flasche in einem Raum mit vier Dimensionen nicht stattfinden würde. Nun ist es schwierig, sich vier Raumdimensionen überhaupt vorzustellen.
Vorstellen kann man sich aber etwa Folgendes: Grundsätzlich ist es möglich, aus einer Raumdimension (einer Gerade, auf der er es nur vor- und zurückgeht) in zwei Raumdimensionen zu wechseln, indem man die Gerade krümmt.
Genauso lässt sich dies noch gut nachvollziehen: Bewegt man sich in zwei Raumdimensionen, so ist dort zwar alles flach, aber man kann immerhin Dreiecke oder Quadrate zeichnen. Diese wiederum lassen sich ebenfalls krümmen bzw. zusammenkleben und dann falten: Zack, befindet man sich in einem Raum mit einer weiteren Dimension.
Theoretisch zumindest ist vorstellbar, dass sich solche Vorgänge in höhere Dimensionen wiederholen lassen.
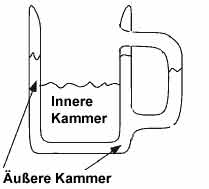
Grafik zur Kleinschen Flasche als Bierhumpen
Wie man aus zwei Möbiusbändern eine Kleinsche Flasche macht, sieht man in folgendem Video:
Noch viel mehr Tricks mit ein paar Papierstreifen, gibt es in diesem Video.
Wie füllt man eine Kleinsche Flasche mit einer Flüssigkeit?